Author: Vignesh Pagadalu

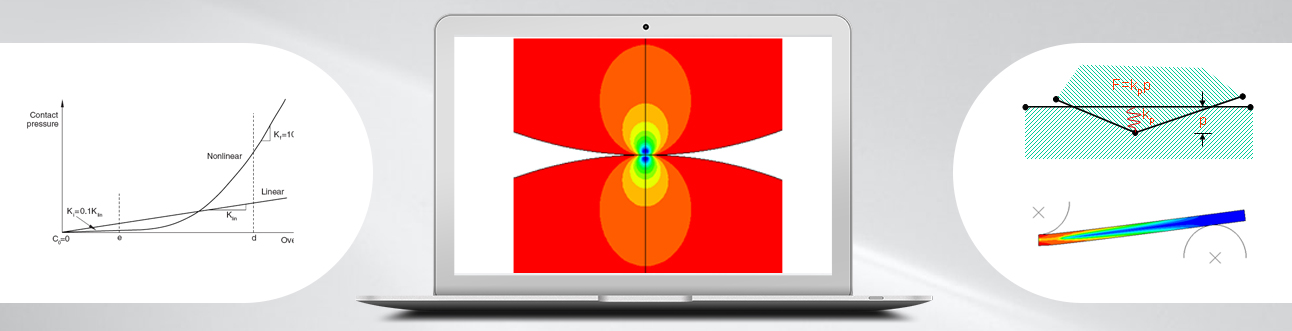
There are two primary methods through which normal direction contact constraints can be enforced in Abaqus/Standard: the traditional direct Lagrange multiplier method and a penalty-based method. The fundamental difference between the two methods is that the Lagrange multiplier method exactly enforces the contact constraint by adding degrees-of-freedom to the problem while the penalty method approximately enforces the contact constraint…

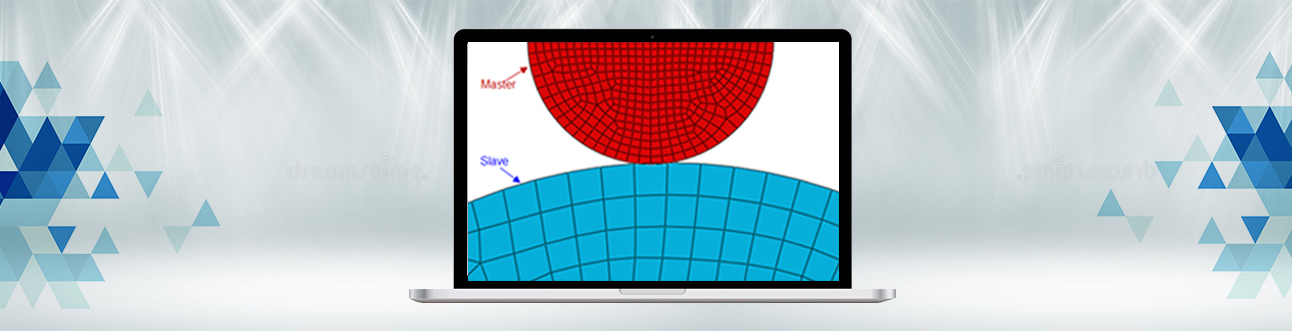
There are three methods of contact constraint enforcement that are available in Abaqus/Standard: The direct Lagrange multiplier method, The augmented Lagrangian method, and The penalty method In this blog, the differences between direct and augmented Lagrangian methods are focussed. Within the context of the classical “hard” contact problem, the direct and augmented Lagrangian methods differ as follows:…

A nonlinear static problem can be unstable as a result of global buckling or material softening. If the load-displacement response of the model seems to be reaching a load maximum and there is the possibility of global instability or negative stiffness, two approaches to solving the problem can be used — static or dynamic analysis. If the…