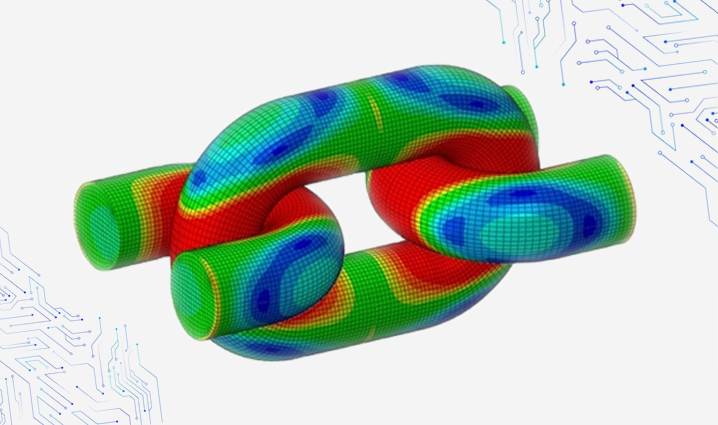
How to Enforce Contact Constraints using Augmented Lagrangian Method in Abaqus/Standard?

There are three methods of contact constraint enforcement that are available in Abaqus/Standard:

• The direct Lagrange multiplier method,
• The augmented Lagrangian method, and
• The penalty method

In this blog, the differences between direct and augmented Lagrangian methods are focussed.

Within the context of the classical “hard” contact problem, the direct and augmented Lagrangian methods differ as follows:

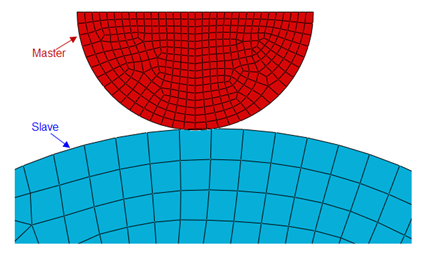
Direct method:

• Enforces the contact constraint exactly so that no penetration of the slave nodes into the master surface is allowed.

Augmented Lagrangian method:

• Enforces the contact constraint approximately using the penalty method. The penalty stiffness is scalable.
• Non-zero penetration of the slave nodes into the master surface is allowed and penetration tolerance is adjustable.
• Once solution convergence is obtained, if a slave node penetrates the master surface by more than the relative penetration tolerance of 0.1% (default setting) of the characteristic interface length, the contact pressure is “augmented”. Iterations continue again until convergence. The solution is accepted when the penetration tolerance is accepted.
• Can sometimes be more expensive than the Lagrange multiplier approach as a result of the augmentation scheme and additional iterations.

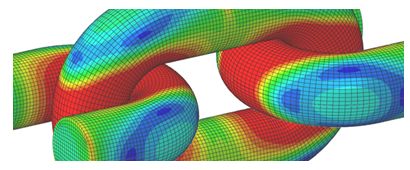
In general, the approximate nature of the augmented Lagrangian contact constraint can simplify the resolution of difficult contact problems and sometimes allow a solution to be found when the exact, Lagrange multiplier constraint is too restrictive. With the ability to scale the penalty stiffness and the penetration tolerance, the contact constraint can be relaxed to facilitate convergence; however this must be done with caution and the results must be carefully checked for excessive penetration of the contact surfaces. More specific situations where this approach can help include:

1. Very different mesh densities on contact pair surfaces

Non-uniform contact pressure distributions are more likely to occur when very different mesh densities are used on the two deformable surfaces making up a contact pair. If the Lagrange multiplier method is used, the non-uniformity can be particularly pronounced, and oscillations and spikes in the contact pressure may occur, when both surfaces are modelled with second-order elements (including modified, second-order tetrahedral elements). Smoother contact pressures may be obtained for surfaces modelled with second-order tetrahedral elements by using the augmented Lagrangian approach.

2. Over-constraint problems

An over-constraint occurs when a contact constraint on the displacements, temperatures, electrical potentials or pore fluid pressure at a slave node conflicts with a prescribed boundary condition or other kinematic constraint on that degree of freedom at the node. Specified boundary conditions on the master surface nodes typically do not cause over-constraints. Specified boundary conditions on slave nodes may create an over-constraint.

Over-constraints can be avoided only by changing the contact definition or the boundary conditions. Over-constraint problems may also be alleviated by using the augmented Lagrangian contact constraint enforcement method. While this may help in certain difficult situations, it is generally preferable to remove the source of the over-constraint.

Vignesh Pagadalu

Mr Vignesh P has done his B. Tech in Mechanical Engineering from Guru Nanak Engineering College (Hyderabad) which is affiliated to JNTU, Hyderabad. He has done his Masters in Science in Automotive Engineering from M.S Ramaiah School of Advanced Studies (Bangalore) affiliated to Coventry University, United Kingdom. He has a total experience of 6.5 years in FEA domain. He has worked on software solutions like Abaqus, Ansys, and Hypermesh. He has handled projects like stent deployment simulations, seismic analysis of dams, optimization of industrial planetary gearbox, etc. He has been with EDS Technologies Pvt. Ltd. for more than 5 years helping customers to develop methodologies for their projects, supporting customers/users on their queries, trainings etc. of both academia (IITs, NITs) and commercial customers.