ABAQUS: DISCRETE ELEMENT METHOD

The computation of effect and motion of a large group spherical particles, where the particles interact with one another and with other surfaces/flow is known as discrete element method (DEM). Granular particles can be simulated in Abaqus using DEM in Abaqus/Explicit Analysis. Abaqus also has another technique to model particles and the technique is known as Smoothed Particle Hydrodynamics (SPH). The major difference between DEM and SPH is that in SPH technique, the particles collectively have continuum behaviour whereas in the DEM technique, the particles cannot undergo a large complex deformation by themselves. Also, DEM technique is a much simpler method.

DEM particles are rigid single-node elements with a certain radius. Particle nodes have degrees of freedom for translational motion and rotation, so considering friction, the latter can significantly affect behaviour, through general contact method. For DEM particles, a contact penalty process is used, which introduces flexibility into the particle system. This correspondence can be used to model the macroscopic stiffness of the filled granular material. Alternatively, the Hertz contact method can be used for particle interaction.

DEM debris may be initialised in the beginning of the analysis, or may be generated all through the analysis. When generated, a random radius, primarily based totally on a user-specified chance density function, may be assigned to every particle. To analyse more complicated shapes in place of easy spheres, more than one DEM debris may be mixed in a cluster the usage of MPC constraints. Clusters aren’t well suited with the particle generator.

Each DEM particle is modelled with a single node element type of PD3D.  The PD3D element type have displacement and rotational degrees of freedom. When friction is considered for a study, the rotational degree of freedom of the discrete element particles has a considerable effect on the contact interactions.

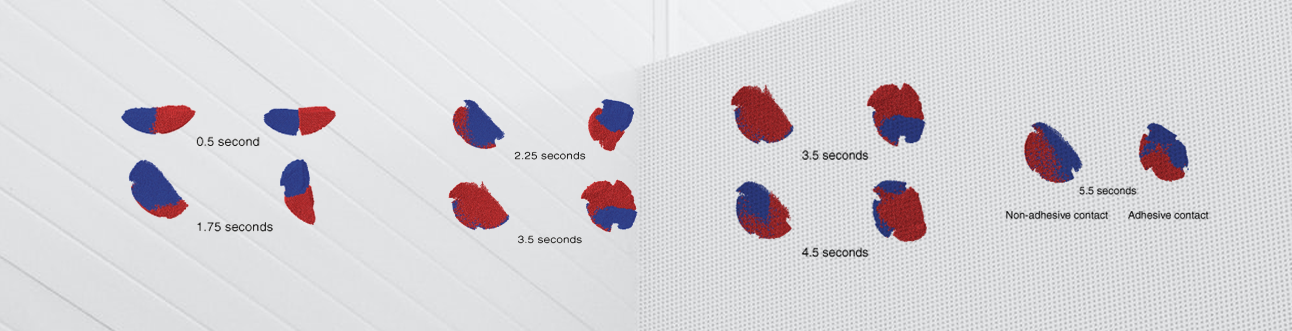
Interaction between Particles

Let us consider three instances of particles in contact as shown in the above figure. The 3 instances display undeformed spheres simply touching, deformed spheres driven closer to each other with contact strictly enforced, and rigid spheres penetrating each other. The distance among the facilities of the spheres is the identical for the middle and right instance as shown in figure above. The middle instance of deformed spheres with no penetration is of physical behaviour. The right instance of rigid spheres penetrating each other is a typical DEM approximation.

If the variable δ is defined as:

δ=r1+r2−d,

where r1 and r2 are the radii of the two spheres and d is the distance between the sphere centres,  when the undeformed spheres are just touching then δ=0  and  if the distance between the sphere centres is less than the combined radii the δ>0 . For the DEM approximation, δ corresponds to the maximum penetration distance between the particles. If the contact stiffness is tuned i.e., contact force v/s penetration, then the accuracy of some DEM applications can be improved. Also, tuning helps to replicate the Hertz contact solution for DEM particles.

Why Use DEM?

• Each DEM particle has individual rotational, positional, radial and momentum vectors that can be easily calculated.
• Simulating DEM method is quite simpler than SPH method and consists of initialisation, time stepping and post processing.
• DEM can be ideally used for modelling granular matter, powders, rock masses, particle packing, particle flow, particle fluid interaction, colloids etc.

Applications of DEM

• Mixing of Chemicals
• Pharmaceuticals
• Powder Metallurgy
• Ceramics
• Food industry
• Agriculture
• Geophysics/Seismology
• Rock fracture
• Soil Mechanics
• Ice blocks floating into bridge supports
• Mining
• Mineral Processing
• Oil and Gas

• DEM is used to study micromechanical level of analysis describing every single position, rotation and velocity for every single particle.
• Accurately model granular and discontinuous materials using DEM to validate models virtually thereby saving a lot of costs that would other incur for the physical testing.
• DEM can be coupled with CFD and FEM to model progressive fracture.

Pratik Deshpande

Pratik is a CAE analyst with a Master’s Degree in Mechanical Engineering from New Jersey Institute of Technology, New Jersey. At EDST, Pratik is responsible for technical initiatives for SIMULIA across industry segments. He works very closely with strategic customers, understanding their design requirements and provide specific workflows with SIMULIA products on mechanisms, FSI, Vibration, Co-Simulation, Fatigue and Failure Models. He had worked with Detroit Engineered Products Inc., Michigan, as an Applications Engineer and as a CAE Lead Research Engineer with Light weight manufacturing systems, General Motors.